Batch 2 - Class 310 - Topology - Toroidal Chess
zoom: send meeting Id and password
Start recording
Preclass Exercise:
- (in class)
Attendance: Anika, Vansh, Shikhar, Rhea Chadha, Ryan Chadha, Adyant, Aarushi, Ekagra, Ayush, Dhriti, Advay, Tarush, Kabir, Nikhil, Yatharth, Aneesh, Anant, Raghav, Siddhant, Siddharth
Class Notes:
Revision
- Cutting Cylinders and Mobius strips
- Tic-Tac-Toe
- Mathematical model of cylinder, mobius strip, torus etc.
- 3 Utilities problem
- Topological equivalence
- Graph coloring
Toroidal Chess
In a normal chess board on a plane, how many bishops are required to cover the entire board?
Let us imagine a chess which has been folded in form of a torus, i.e. we have joined the left and right edges, and the top and bottom edges. It looks something like the following:
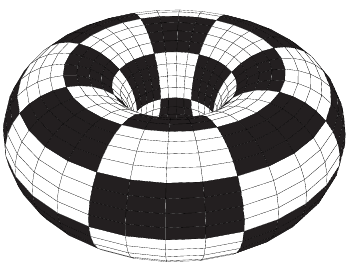
- What if we placed a bishop on one of the squares. Where all can it move?
- How many squares can a bishop move to in normal chess? How about a toroid? Does it depends on where the bishop starts?
- Why 14 squares? What would happen on a 6x6 board? 10x10 board? Is there a pattern?
- How does that change the power of the bishop?
- Wait, what if the bishop was on a rectangular board? How many squares could it hit on a 8x6 board?
- The bishop always stays on the same color. Is that true? What would happen on a 7x5 board? How many squares can the bishop hit?
- Can you find some general rules on how many squares the bishop will hit?
- When does its power come in full force?
Lets move away from the bishop. How about the queen?
- How many queens does it take to dominate a normal chess board? Dominate means attacking all squares including the square the queen is on
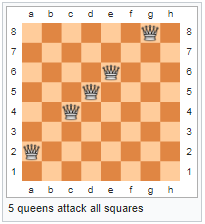
- How many queens does it take on a toroidal chess board to attack all squares?
- Many answers are available with 5 queens. Some samples below
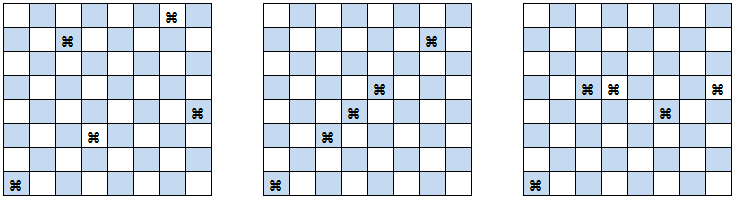
What about knights? How many knights do we need to attack all squares, including the ones that the knights are sitting on?
- How many knights does it take to dominate a normal chess board? With and without attacking the occupied squares?
.png)
- What's the minimum possible number on a toroidal chess? Can you do that in the minimum possible? What must be the distribution across white and blacks? Does it matter where you place the first one? Where can you place the second one? Can you devise the pattern based on coverage?
.png)
Homework Problem:
Imagine folding a 8x8 chessboard into a mobius strip. Explore the paths of a bishop on the same (you may assume that the initial strip was printed back to back). You can rollover the edge of the strip when you encounter it.
References: